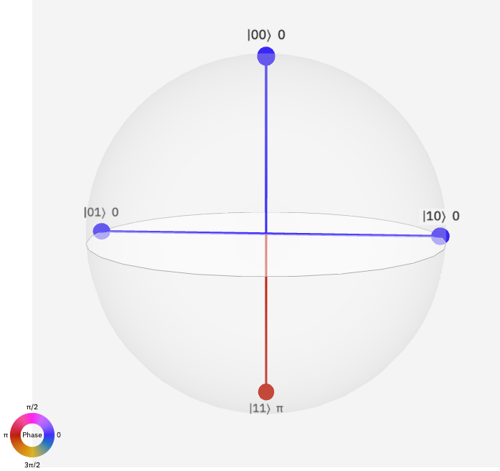
Each node on Q-sphere represents a basis state. The Q-sphere together with its color panel represent a quantum state.
The definition of Q-sphere:
The q-sphere represents the state of a system of one or more qubits by associating each computational basis state with a point on the surface of a sphere. A node is visible at each point. Each node’s radius is proportional to the probability ($P_k$) of its basis state, whereas the node color indicates the quantum phase ($\phi_k$).
The nodes are laid out on the q-sphere so that the basis state with all zeros (e.g., is at its north pole, and the basis state with all ones (e.g. $|111\rangle$ ) is at its south pole. Basis states with the same number of zeros (or ones) lie on a shared latitude of the q-sphere (e.g.$|100\rangle, |010\rangle,|001\rangle$ ). Beginning at the north pole of the q-sphere and progressing southward, each successive latitude has basis states with a greater number of ones; the latitude of a basis state is determined by its Hamming distance from the zero state. The q-sphere contains complete information about the quantum state in a compact representation.
For example 2-qubits state $|\psi> = |00\rangle + |01\rangle+ |10\rangle - |11\rangle$ can be described by this Q-sphere:
For a 2-qubits state, there are intotal 4 basis states, thus there are at most 4 nodes on the Q-sphere and the position of those nodes(basis states) are fixed. The only thing you can change is the color which represent the phase factor in front of the basis state.
In your example, the nodes are not located at the equator, thus there must be more than 2 qubits.