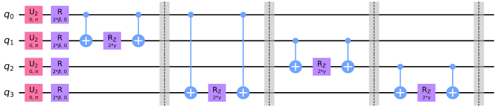
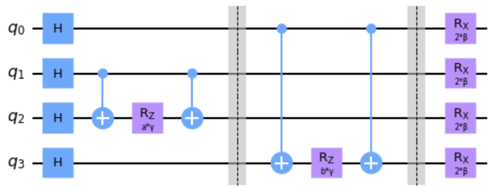
From my understanding, the parameters used in QAOA circuit (eg, beta for mix H and alpha for cost H) are non-deterministic. We can use different techniques to initialize these parameters and they will be updated according to the optimizer. The parameters are used in Rz gate. Please correct me if I didn't understand it correctly!
Let's say we have a weighted graph and we want to use QAOA to solve maxcut problem, the cost Hamiltonian H_c = 0.5 * IZZI + 0.5 * ZIIZ +...
My question is, how to demonstrate the weights (i.e, 0.5 in this case) in our circuit? Is there a different approach to construct a QAOA circuit for a weighted graph compared to an unweighted graph?