What is minimum weight perfect matching in a toric code decoder?

I have come across the minimum weight perfect matching algorithm in a surface code decoder as a benchmark method. Could anyone explain why do we need it and how does the algorithm work in the surface code?

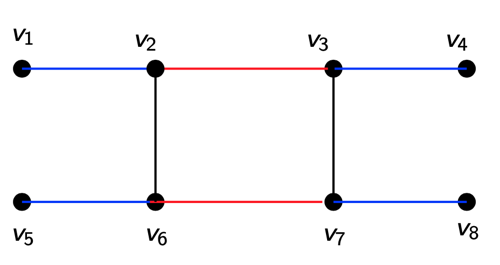
Minimum weight perfect matching

• Given an undirected graph $G(V,E)$, a matching $M$ in $G$ is a subset of edges such that no two edges in $M$ share an end point.
• If the edges in $M$ cover all nodes in $G$, then it's called a perfect matching
  For example,
  
  The blue edges form a perfect matching
• If $G$ is a weighted graph, there are many perfect matching we can choose and we can minimized the total weight in $M$.

1D repetition code

Surface code is less intuitive, we can take a look at 1 dimensional repetition code first.
In 1D, the error syndromes are also in 1D. We can map the error syndrome to a graph by mapping detected stabilizers to nodes and the distance between them to be weighted edges.

If we are able to find a matching, then the qubits within the matching are which have errors. We can see there are multiple ways to choose matching(blue edges), but the minimum weight perfect matching corresponding to the most likely happened errors in the repetition code.

[1] Reference slides