What is the density matrix of a GHZ gate?

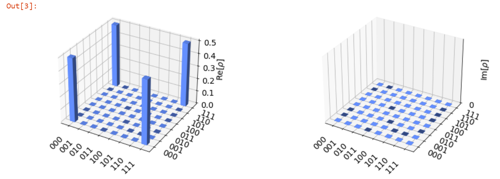
By definition, the GHZ state is

$$
\ket{GHZ} \equiv \frac{1}{\sqrt{2}} (\ket{000}+\ket{111}),
$$
so the density matrix is
$$
\rho_{GHZ} = \ket{GHZ} \bra{GHZ} = \frac{1}{2} (\ket{000}\bra{000}+\ket{111}\bra{000}+\ket{000}\bra{111}+\ket{111}\bra{111}).
$$

You can check this in qiskit as well:

from qiskit import QuantumCircuit
from qiskit.quantum_info import DensityMatrix
from qiskit.visualization import plot_state_city

# Define a quantum circuit with the GHZ gate 
ghz = QuantumCircuit(3)
ghz.h(0)
ghz.cx(0,1)
ghz.cx(0,2)

# Translate GHZ circuit into density matrix
ghz_state = DensityMatrix.from_instruction(ghz)

# Plot the GHZ density matrix
plot_state_city(ghz_state)