ZZFeatureMap entanglement setting in qiskit

When doing quantum machine learning in qiskit, such as using support vector machine for the classification of random 2D data, what is the principle of choosing the entanglement setting in ZZFeatureMap? For example, does full entanglement always give better perdition accuracy than linear? Do I have to consider the feasibility of physical realization in a certain backend? What about run time in these two settings?

In order to answer your question, we need to know:
1. What is a quantum feature map?
2. Where and how a quantum feature map is used in QML?
3. What is the difference between different entanglement layer structures linear vs full?
4. How a quantum feature map is realized in a real quantum hardware?
5. Run time comparison for linear and full entanglement layer?

1. What is a quantum feature map?
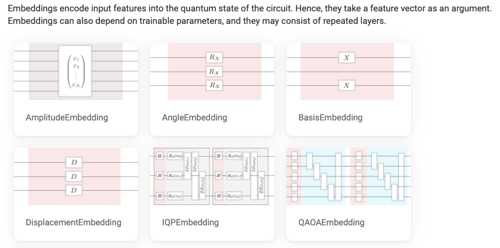
For the background knowledge, quantum feature maps are widely used in the process of quantum embedding. This process encodes classical data $\vec{x}$ into quantum data $|\psi(\vec{x})\rangle = U(\vec{x})|0\rangle^{\otimes n}$ via a parametrized quantum circuit (PQC) $U(\vec{x})$ (in the context of QML). For a brief review, check Pennylane's post. Notably, the authors discuss the relation between encoding data multiple times and the universality of QML models in ref [1] by considering the accessible frequencies $\Omega$ in a partial Fourier series $f(\vec{x}) = \sum_{\omega \in \Omega} c_\omega e^{i\omega x}$.

For the frequently used quantum feature maps, please check:
- Embedding templates from Pennylane
- Qiskit Circuit Library -> Data encoding circuits

Note: Similar to the choice of variational ansatz in VQE, there is no general recipe for choosing the best quantum feature map!! Unfortunately, most QML algorithms are heuristics which means you have to tune the model parameters and see how it actually behaves. One can also design a meta-learning algorithm to automatically construct better quantum feature maps [2].

2. Where and how a quantum feature map is used in QML?
It is usually used in quantum supervised learning like a Variational Quantum Classifier and Quantum Kernel Methods. From my experience, a full entanglement layer does not always give better perdition accuracy in quantum classifiers. But the idea behind is a complicated entangling layer is hard to simulate classically which could bring potential quantum advantage.

3. What is the difference between different entanglement layer structures linear vs full?
According to Qiskit's API on the TwoLocal circuit:
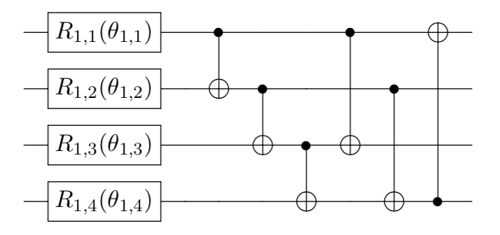
- full entanglement is each qubit is entangled with all the others.
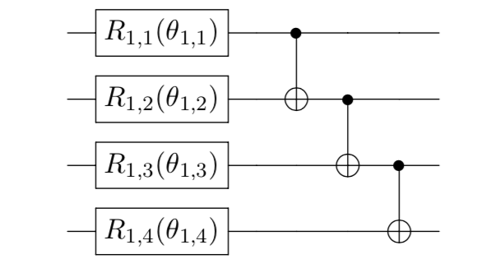
- linear entanglement is qubit 𝑖 entangled with qubit 𝑖+1, for all 𝑖∈{0,1,...,𝑛−2}, where 𝑛 is the total number of qubits. Also known as the hardware-efficient ansatz [3].
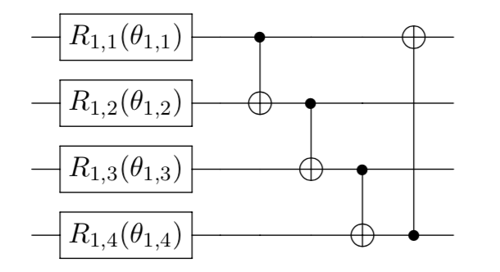
- circular entanglement is linear entanglement but with an additional entanglement of the first and last qubit.

For example, considering the following 4-qubit quantum circuit with full/linear/circular entanglement:

4. How a quantum feature map is realized in a real quantum hardware?
Similar to other quantum circuits, the feature map eventually will be transpiled into physical signals (microwave pulses for superconducting qubits). The issue happens when considering a full entanglement layer. Since some physical qubits are not connected with each other (limited by the topology/coupling map of a specific quantum device), we cannot directly apply two qubit gates on those qubits and it will take a longer time to go through the transpiler to resolve this by inserting SWAP gates. This is usually known as the Qubit Mapping Problem for NISQ devices [4].

Note: For this device, $q_0$ and $q_9$ are not connected so we cannot directly apply two qubit gates on them.

5. Run time comparison for linear and full entanglement layer?
Since there are usually more two qubit gates in the full entanglement layer than the linear structure, the former naturally takes a longer run time. Besides, too much entanglement in the QML model will also induce the notorious Barren Plateau issue [5].

Reference:
[1] Schuld, Maria, Ryan Sweke, and Johannes Jakob Meyer. "Effect of data encoding on the expressive power of variational quantum-machine-learning models." Physical Review A 103.3 (2021): 032430.
[2] Altares-López, Sergio, Angela Ribeiro, and Juan José García-Ripoll. "Automatic design of quantum feature maps." arXiv preprint arXiv:2105.12626 (2021).
[3] Kandala, Abhinav, et al. "Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets." Nature 549.7671 (2017): 242-246.
[4] Li, G., Y. Ding, and Y. Xie. "Tackling the Qubit Mapping Problem for NISQ-Era Quantum Devices. arXiv e-prints." arXiv preprint arXiv:1809.02573 (2018).
[5] Marrero, Carlos Ortiz, Mária Kieferová, and Nathan Wiebe. "Entanglement induced barren plateaus." arXiv preprint arXiv:2010.15968 (2020).