Background
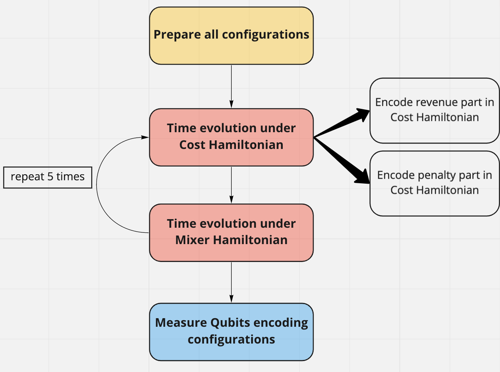
In this post, we will discuss how to implement a quantum circuit that solves an optimization problem without classical optimization, based on this adiabatic quantum computation framework. In other words, the circuit gives a good approximate solution in a single run. This is contrary to the well-known QAOA quantum-classical hybrid approach.
(The following answers are also solutions to 2021 Qiskit Fall Challenge Problem 4c)
Battery Revenue Optimization Problem
Battery storage systems have provided a solution to flexibly integrate large-scale renewable energy (such as wind and solar) in a power system. The revenues from batteries come from different types of services sold to the grid. The process of energy trading of battery storage assets is as follows: A regulator asks each battery supplier to choose a market in advance for each time window. Then, the battery operator will charge the battery with renewable energy and release the energy to the grid depending on pre-agreed contracts. The supplier therefore makes forecasts on the return and the number of charge/discharge cycles for each time window to optimize its overall return.
How to maximize the revenue of battery-based energy storage is a concern of all battery storage investors. Choosing to let the battery always supply power to the market which pays the most for every time window might be a simple guess, but in reality, we have to consider many other factors.
What we can not ignore is the aging of batteries, also known as degradation. As the battery charge/discharge cycle progresses, the battery capacity will gradually degrade (the amount of energy a battery can store, or the amount of power it can deliver will permanently reduce). After a number of cycles, the battery will reach the end of its usefulness. Since the performance of a battery decreases while it is used, choosing the best cash return for every time window one after the other, without considering the degradation, does not lead to an optimal return over the lifetime of the battery, i.e. before the number of charge/discharge cycles reached.
Therefore, in order to optimize the revenue of the battery, what we have to do is to select the market for the battery in each time window taking both the returns on these markets (value), based on price forecast, as well as expected battery degradation over time (cost) into account.
Problem Setting
Here, we have referred to the problem setting in de la Grand'rive and Hullo's paper [1].
Considering two markets $M_{1}$ , $M_{2}$, during every time window (typically a day), the battery operates on one or the other market, for a maximum of $n$ time windows. Every day is considered independent and the intraday optimization is a standalone problem: every morning the battery starts with the same level of power so that we don’t consider charging problems. Forecasts on both markets being available for the $n$ time windows, we assume known for each time window $t$ (day) and for each market:
the daily returns $\lambda_{1}^{t}$ , $\lambda_{2}^{t}$
the daily degradation, or health cost (number of cycles), for the battery $c_{1}^{t}$, $c_{2}^{t}$
We want to find the optimal schedule, i.e. optimize the lifetime return with a cost less than $C_{max}$ cycles. We introduce
We introduce the decision variable $z_{t}, \forall t \in [1, n]$ such that $z_{t} = 0$ if the supplier chooses $M_{1}$ , $z_{t} = 1$ if choose $M_{2}$, with every possible vector $z = [z_{1}, ..., z_{n}]$ being a possible schedule. The previously formulated problem can then be expressed as:
Author Introduction
Yusheng Zhao, graduated from Physics and Astronomy Master Program of Stony Brook University in 2020. He enjoys coding and learning about quantum computing. He achieved Top 10 scores in IBM Quantum Challenge Fall 2021 among over 1,200 participants.